Sigmoid 函数

Posted by RAIS on 2021-01-17

前言

Sigmoid 函数（Logistic 函数）是神经网络中非常常用的激活函数，我们今天来深入了解一下 Sigmoid 函数。

函数形式

$$
S(x)=\frac{1}{1+e^{-x}}
$$

$$
y=\begin{cases}
1, 当 S(x)\geq0.5 \\
0, 当 S(x)<0.5
\end{cases}
$$

$$
S(x)’=\frac{e^{-x}}{(1+e^{-x})^2}=S(x)(1-S(x))
$$

函数图像

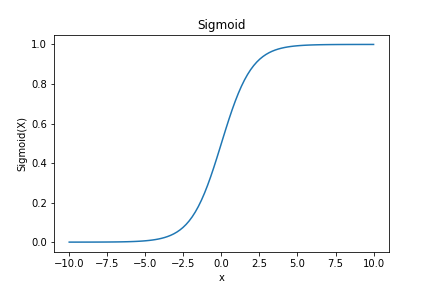
Sigmoid

代码实现

代码运行：Colab

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import matplotlib.pyplot as plt
import numpy as np
import math

x = np.linspace(-10, 10, 100)
z = 1 / (1 + np.exp(-x))

plt.title("Sigmoid")
plt.plot(x, z)
plt.xlabel("x")
plt.ylabel("Sigmoid(X)")

plt.savefig("sigmoid.png")
plt.show()
plt.close()

性质及问题

函数值 S(x) 的值域为 (0, 1)，常用于二分类问题，函数平滑，易于求导。但是作为激活函数，其计算量大，反向传播求误差梯度时，求导有除法，容易出现梯度消失的情况，在输入接近于正无穷或负无穷时，梯度趋近于 0，发生梯度弥散（随着网络层数的增加，使用反向传播算法计算梯度时，从输出层到最初几层，梯度消失的非常明显，造成整体损失函数对最初几层的权重的导数非常小，这样在使用梯度下降算法时，最初几层权重变化非常慢，甚至无法学习到有用的特征）。因为 Sigmoid 函数值大于 0，因此权重更新只能朝着一个方向更新，可能影响收敛速度。

总结

Sigmoid 函数是神经网络中一种非常常用的激活函数，被广泛应用于逻辑回归，在统计学，机器学习领域有其广泛应用。




FRIENDS